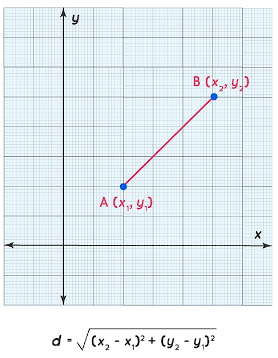
Euclidean distance is the length of the line segment between two points in Euclidean space. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem. It is a simple formula enough to be calculated by hand but powerful enough to be used in Machine Learning and Artificial Intelligence applications for clustering and classification models. We can also use the Euclidean distance formula to find the distance between points in higher dimensions, such as three-dimensional space.
For example, if the points are (x1, y1) and (x2, y2), then the Euclidean distance between them is given by:
d = SQRT((x2−x1)^2 + (y2−y1)^2) or,
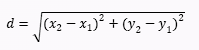
This is so useful that in Python provides a built-in method named dist() that returns the Euclidean distance between 2 points. Just import the math library, and code: math.dist(A, B) # where a A and B are each a 1D array (list) of 2 values in x,y sequence.
Here’s my quick Python app that takes the coordinates of two points from the user, and shows the Euclidean distance between them. Try it out right here on the page below.
(press 
to run it, enter your coordinates)
Note that the Euclidean distance has the same units as the positions are measured in. The distances are measured as the crow flies in the projection units of the raster, such as feet or meters, and are computed from cell center to cell center.
▛Interested in creating programmable, cool electronic gadgets? Give my newest book on Arduino a try: Hello Arduino! 
▟