Recently, I was reading a post about an mathematical formula when applied to any number (positive integers) will end up at 1, no matter odd or even. It’s called the 3n+1 problem or the Collatz Conjecture.
So, of course, I tested the theory and sure it works. Actually, when you think about it, it’s no mystery that it works. In fact, my wife (who’s not a mathematician by any stretch) proved that we can achieve the convergence in a MUCH more efficient way by simply n+1 (instead of 3n+1) for the odd numbers, and keeping 1/2 for even numbers.
First, let’s recap the Collatz/3n+1 algorithm…(you can see a youtube video on that here)
Here’s the idea: Pick any whole, positive number, and if it’s even then divide it by 2. Keep doing it and you’ll end up at the number 1. If the starting number or any number along the steps is an odd number, then multiply it by 3 and add 1 (3n+1). Repeat the process until you converge to 1. Obviously, if you start with an odd number, and you do 3n+1, you’ll end up with an even number, then apply the same rule above for even number (i.e. divide by 2), and if you end up with an odd number after division, you apply the same rule as for the odd number, and so on. Nothing ground-breaking, except indeed you will NOT get stuck at any number (that we know of to-date, or no one had been able to prove such yet).
Let’s Run Some Simple Examples…
Example 1: 5
Start with 5. It’s odd, so the next number we should get is 16 (=3n+1). Then 16 is even, so next we get is 8. Then it’s 4 (=8/2 again), then 2, and finally 1. It took 5 steps ending in the series: 5, 16, 8, 4, 2, 1.
Example 2: 10
Let’s start with 10. After first step (1/2), we get 5. Then we go through the same steps as above since we’re at number 5 as in example 1. After 6 steps, we converge to 1, and the series is: 10, 5, 16, 8, 4, 2, 1.
So What?
Instead of 3n+1, we could do n+1 (and divide by 2 for even numbers as before) and it’s quicker and therefore far more efficient (the larger the starting number, the more efficient it is over 3n+1 method) and requires less computational power as well.
NOTE, that if you try 3n-1 (instead of +1), you will get stuck in a loop. Try it with 7 as starting number. Using 3n-1, you’ll get this series and NEVER converge to 1…this is why: 7-> 20-> 10 -> 5 -> 14 ->7 -> 20 ->10 ->5 -> 14 ->7…FOREVER in a loop.
Automate This!
Let’s compare the 3n+1 method vs our own n+1 method: To make this very efficient and quick, I wrote a quick program to test both 3n+1, and n+1 so I can play with any large numbers in miliseconds. While I’m at it, I’m going to generate the series and keep track of number of steps it took to converge to 1. Here’s the summary of results…the number of steps our n+1 method took are under n+1 column, and steps 3n+1 took are under its 3n+1 column. The results are not even comparable and you NEVER GET STUCK with n+1 method (as you would with 3n-1)!
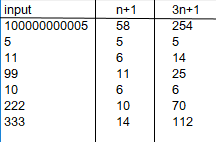
Using my program, we can easily see the number of steps, and the sequence of numbers generated in the process regardless of how large the number is. And then I chart the sequence to visualize the convergence. Two generated charts are shown below. One using n+1, another 3n+1 using the same starting number: 1000000001
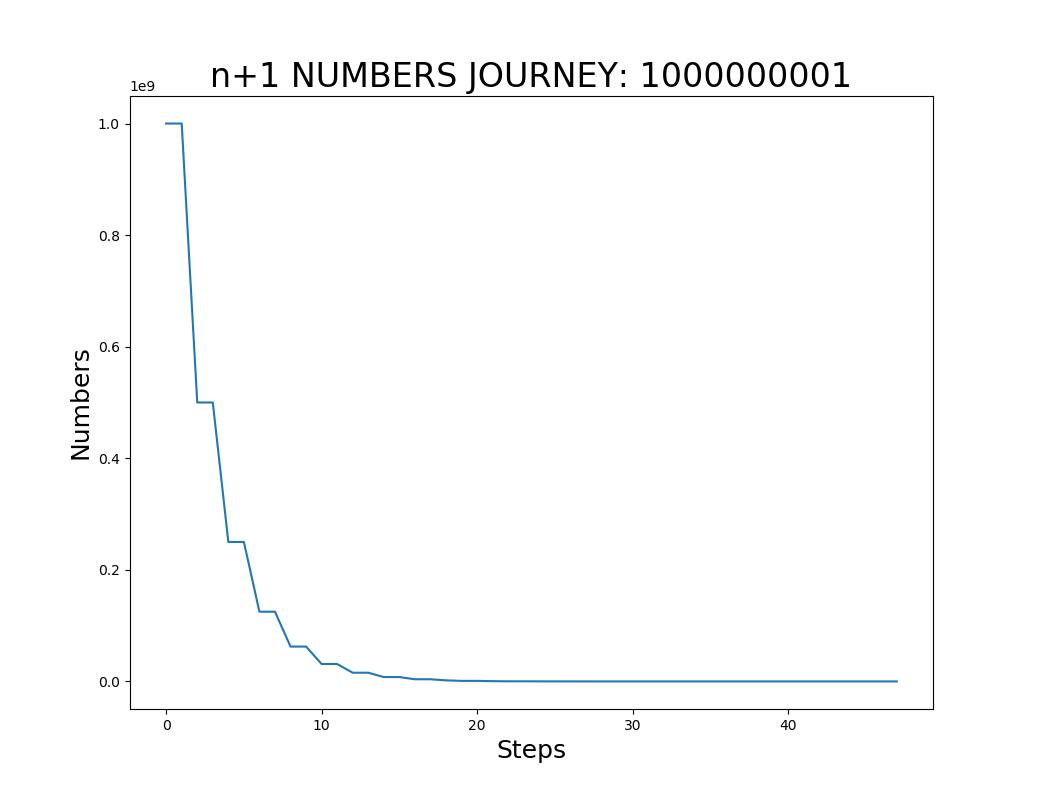
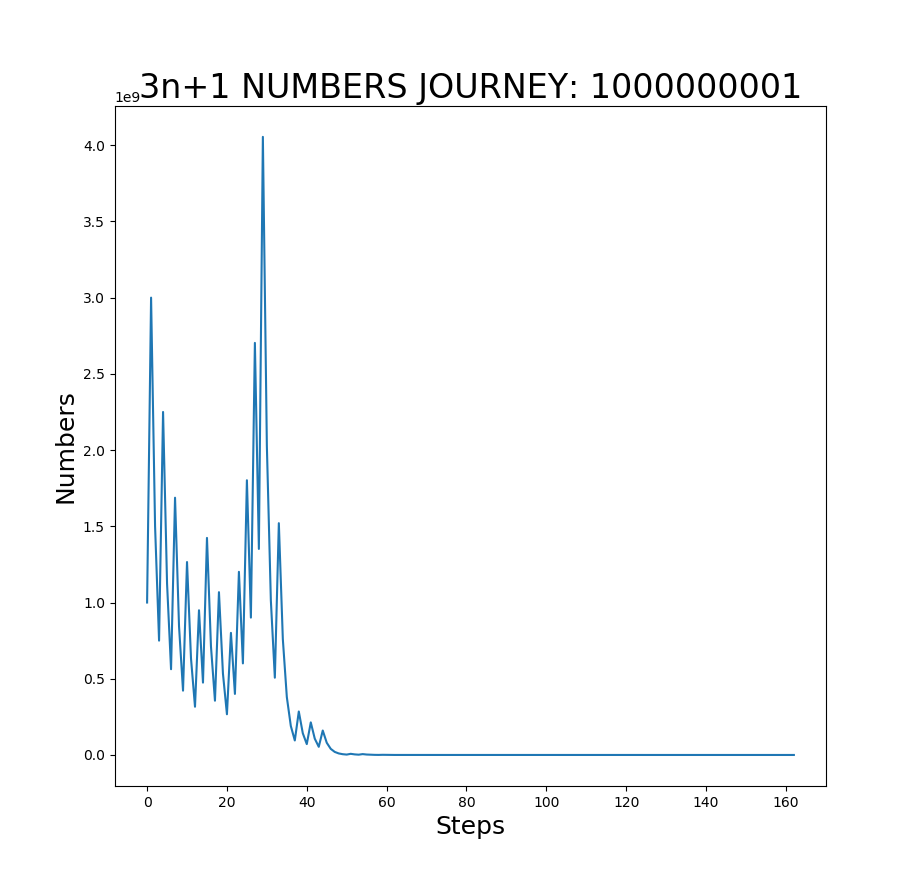
As you can see the converge to 1 took only 47 steps using n+1, and 162 using 3n+1. NO CONTEST.
And So?
I was wondering what all the hype about Collatz Converge had been…it doesn’t really have any real-world application, and even if it did, we created a FAR more efficient method to converge as proven here. However, I was wondering would be possible to re-generate all the sequenced numbers and get to the starting number?
Try it with either 3n+1 or n+1 methods by starting with the number 5, and then create an algorithm that starts at the last number (1) and generates each number in the sequence, in order (reverse order) so that we get from 1 to 5 and generate this series: 1, 2, 4, 8, 16, 5 (see Example 1 above, this series is exact reverse of that since we’re going backward from 1 to 5 instead of 5 to 1).
Collatz couldn’t do it, and no mathematician has been able to do it using mathematical principles that I know of. Also, simply by reversing the math operations is NOT going to get us to the original number. Try it.
And yet, it is possible to do it using logic (I’m not a mathematician) and programming. In my next blog, I’ll explain how it can be done, and how I achieved it. We will raise the bar on this challenge! See the next blog here (Part2).