Here’s the Scenario:
Based on our observations over a month, we find that there are 40 dogs on average in a off-leash park during an hour’s time-frame during the day in its open hours.
We want to find out the chance of having a specific number of dogs at any given time in the park during the day (#1).
And we also want to know the chance of having a maximum number of dogs at any given time in the park during the day (#2).
We want to use this data to determine the cost of maintenance of the park, staffs needed, budget needed, and the hours of operation.
Solution:
We’ll use POISSON.DIST() using the Mean=40. For #1: [specific target], we’ll use probability mass function. For #2: [maximum or <= range], we’ll use cumulative distribution function.
Finally, we’ll visualize it using 2 charts and present the recommendation. Let’s get to work…
The Process:
We will tabulate the data and calculate the probabilities at each trial using mass and cumulative versions of POISSON distribution. It looks like this:
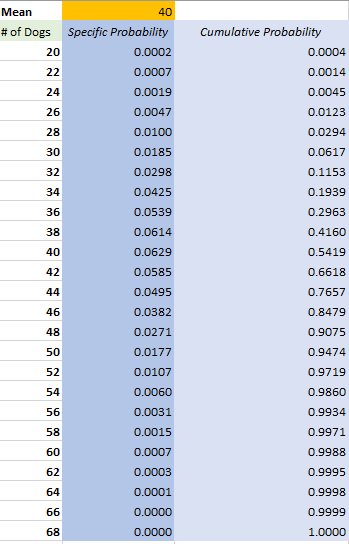
Then we chart the results for each method which look as follows:
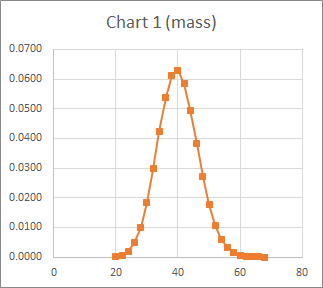
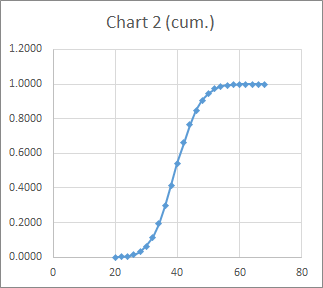
Now we have all the information needed to make a recommendation based on the observation.
Observations:
– There’s about zero chance of having exactly 20, 22…all the way to 26 dogs (mass). Also zero chance, of having 24 dogs or less.
– About zero chance of having 54 or more.
– About 6.3 % chance of having 40 dogs.
– Almost certainly (99%+ probability) of having 56 dogs or less.
– Small chance of 32 dogs, a little higher chance of having 46 dogs (about 3% vs 3.8%).
Recommendation:
Based on these figures, it’s prudent to plan for accommodation of 32 to 46 dogs with room for error and scale.