In this post, I’ll demonstrate implementation of what’s known as a General Tree (not binary tree…that’ll be discussed soon in a different post)…it’s a unique data structure that Queue or Stacks cannot easily handle or at all. The key characteristic of this DS is that it allows for hierarchical data representation and relationships…think, taxonomy.
Real-world uses include: Product categorization in a store; Books, movies categories; organizational chart, and even certain types of family trees.
It’s a tree because it’s analogous to a tree turned upside down. It has a root node (the top-most node) at the top. It can then be connected to other nodes, called children nodes under it. Then the children could have further nodes under the children as children nodes again, and so on. There’s no limit as to how deep the branches can go. The nodes that have no children are the leaf nodes or leaves.
Let’s take a look at a simple tree structure and I’ll identify the key points with labels.
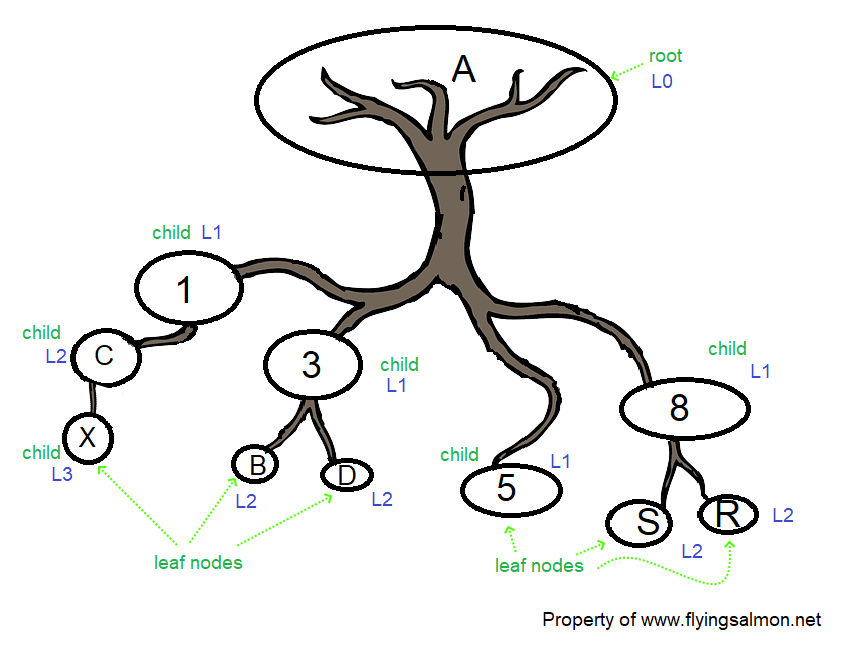
In figure 1, we see an upside down tree with A being the root node (names don’t matter). This tree has 11 nodes total. Node A has 10 children at different levels or tiers. The root level is zero and it increments downward per level. At level 1, we can call those 4 children A’s immediate children and they are nodes 1, 3, 5, 8. These nodes are peers. Then we see some level 1 children have children as well, except node 5. So, node 1 has one child C. Node 3 has B, D. Node 8 has S, R. They can be thought of as grandchildren of node A, and they’re in level 2. Then we also have node X, which is a child of node C. This can be thought of as the great-grandchild of node A, and is at level 3. The nodes that have no children are the leaf nodes as marked in the diagram.
Not that I’m a fan of the royal traditions or care much about them as I live in the USA, we can’t help but know that Queen Elizabeth II is the first to each the Platinum Jubilee milestone…meaning, the 70th anniversary of a British monarch’s reign. That’s incredible! Celebrations are underway all over Great Britain and its monarchy around the world (including Australia, Canada, New Zealand, etc. At any rate, I was curious to see her royal family tree.
I found the following snapshot from BBC.com (full url credit in the image) and I thought why not represent this royal tree in a General Tree Data Structure in Python? That’s exactly what I’ll do below.
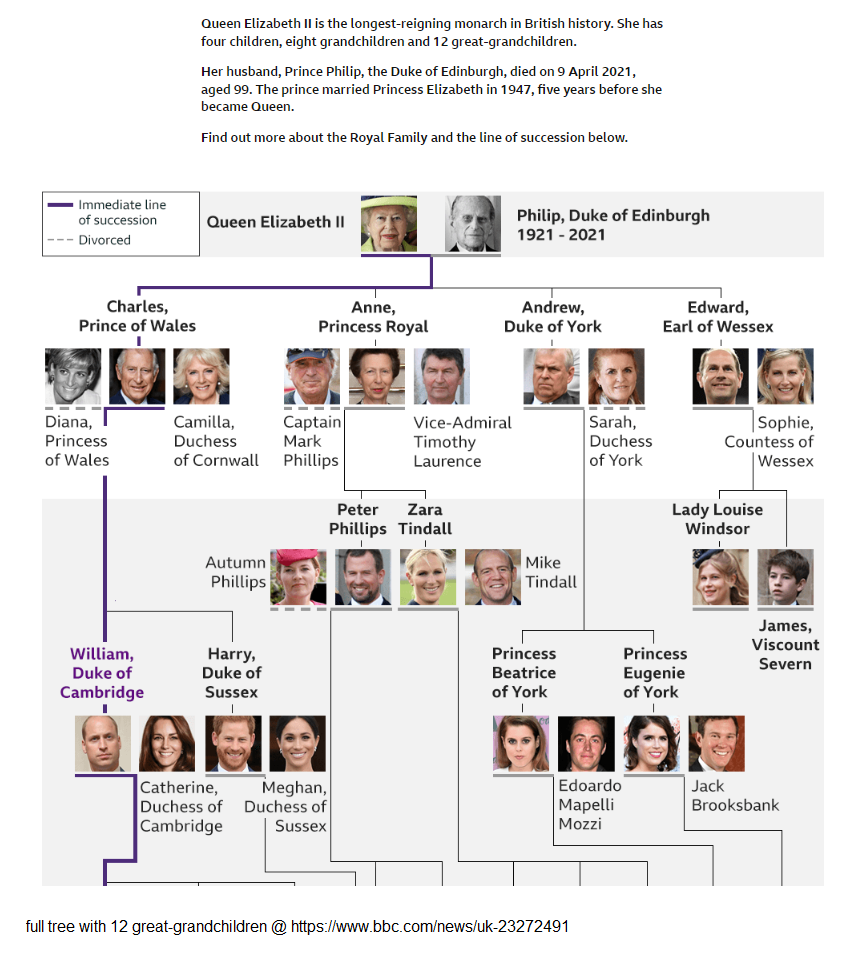
For this exercise, I won’t go deeper than grandchildren. If you want to add great-grandchildren to the tree, please do so on your own as it’s rinse-and-repeat—once you can do up to level 2, you can copy/paste the same code with little modification to any number of levels.
Therefore, all the nodes can be shown simply as:
Elizabeth II : Queen
|___Charles : Prince of Wales
|___William : Duke of Cambridge
|___Harry : Duke of Sussex
|___Anne : Princess Royal
|___Peter Phillips : None
|___Zara Tindall : None
|___Andrew : Duke of York
|___Beatrice : Princess of York
|___Eugenie : Princess of York
where Queen is the root. But some of the nodes are the queen are also parents of other nodes, so withouth getting too fancy or graphical, we can decipher the tree clearly if we can create an output from our program as below:

By the way, if you want how to do true graphical representation with color-coding, shapes, lines, then check out my blog post on network graphs here.
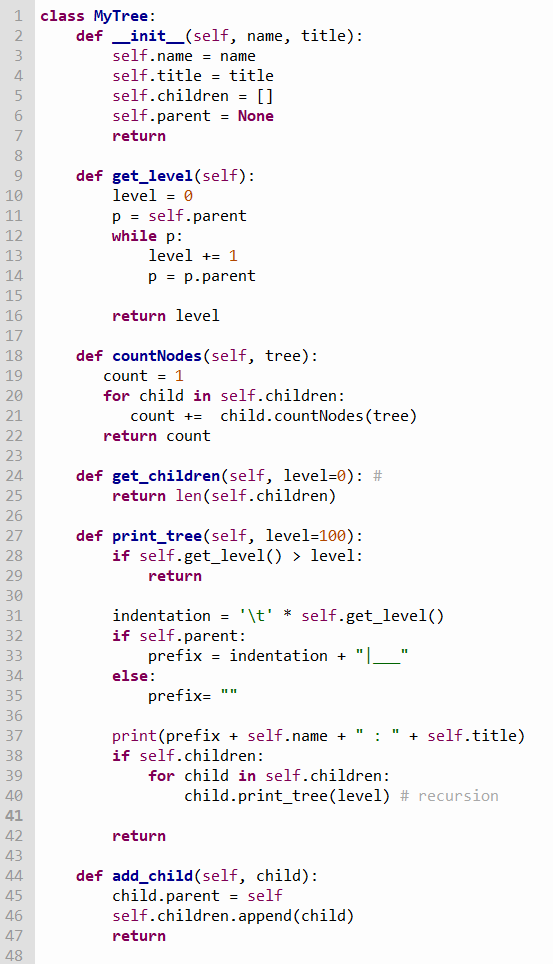
To implement a General Tree in Python, we don’t need any special library. Probably the best approach is OOP (object-oriented programming)…using Classes and methods. So, we want to display the name and title for each node. Then we also need a way to indicate each node’s parent…only the root will have no parent. Then we need to write some methods to help us extract some data from the objects when we instantiate them based on the tree class we create first. That part of the code is shown in Figure 4.
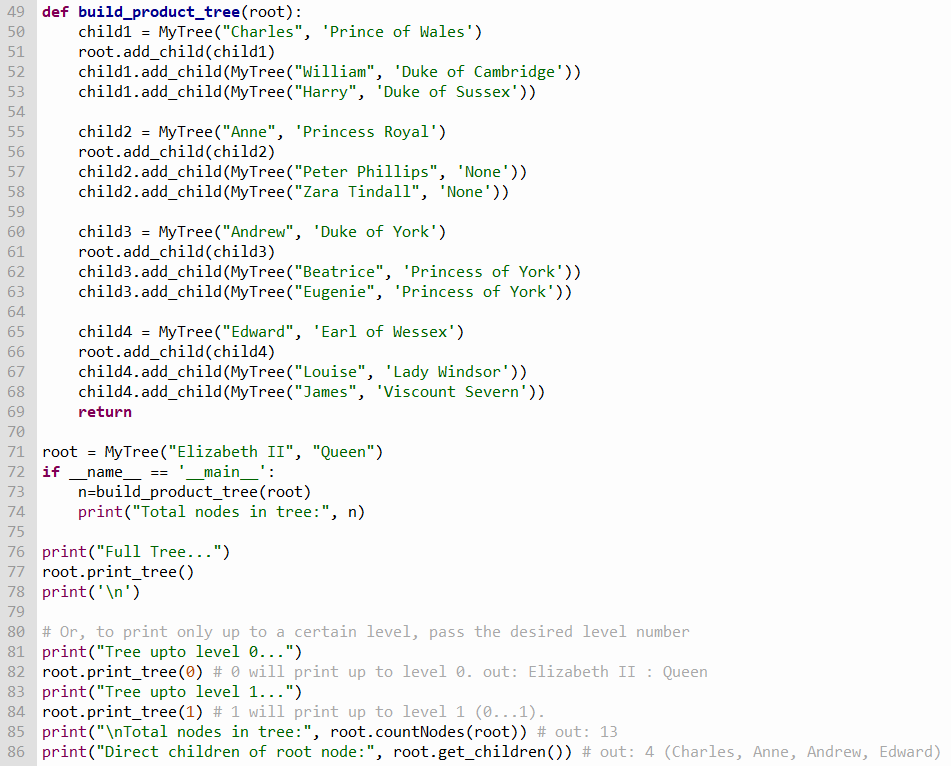
Additionally, I have a helper function build_product_tree() which is not a class method and it just builds the tree. First though, we have to create a tree object based on the class we defined earlier. That’s done in line 71 (Figure 5) and now we save the returned object as root. build_product_tree() takes that object and adds all the immediate children under root node, and then additional children under them (if any…it so happens that they each have exactly 2 children!!). Because there’s a name and title (in most cases), we pass them to the add_child() method as shown in Figure 5.
Most of the code in Figure 4 should be self-explanatory with some knowledge of OOP, but a couple of things may need further explanation.
Recursion is critical for trees. We used in countNodes() method to count all the nodes for the root node in our tree. For each child for the node, we keep incrementing the count by recursively calling it until there are no more children, and finally return that count.
We also have to do recursion to print the tree in print_tree(). This method can optionally take a level (0 to n…see the explanation for Figure 1 for levels). If no level is specified by the caller, it’ll go through the entire tree. If there’s a level specified, it’ll start from the root node and traverse the tree downward until that specified level. This also calls itself (recursion) until there are no more children nodes. Within that, to make the hierarchy using text, I used tab (‘\t’), pipe (‘|’) and underscores (‘___’) as prefix for nodes that are not at root level and how many depends on that node’s level# (0…n). Colon and spaces (‘ : ‘) in line 37 separate the name from the title in our prints.
In line 82, when we call root.print_tree(0), we’re asking for name and title of nodes at level 0, which is the queen herself, so the output will be: Elizabeth II : Queen
In line 84, when we call root.print_tree(1), we’re asking for names and titles of nodes at level 1, which are immediate children of the queen, so the output will be as follows:

When we call root.print_tree() without any parameter, it’ll show our full tree as below:

If we want to get the total number of nodes in the tree, we can call root.countNodes(root) and to get direct children nodes of the root, we can get root.get_children(). The calls in line 85 and 86 do just that. And the output will be:
Total nodes in tree: 13
Direct children of root node: 4get_level() is a clever little helpful method to return the level number as an integer of any node. It works because levels are 0-based, meaning root is level # 0, then its immmediate children are level # 1, and so on. And if we take a node and check how many parents it has, (we use a local varirable level as a counter, and increment it if a parent is found) we get its own level number! For example, if we are at Anne node (in royal family tree above) and count its parents, we see there’s only 1 parent (the queen), so Anne’s level is 1 (while Queen’s is 0). If we take node Zara, we see it has Anne as a parent (so level is 1 at this point), but we continue looking because we have it in a while p: loop (line 12) and we’re reassigning the parent to variable p in each iteration, so it continues upward and finds that Anne has a parent (Elizabeth II) so Zara’s level gets incremented to 2. Then it looks for Elizabeth’s parent and there is none in this royal tree, she’s the queen! The level counter’s final value for Zara node is 2.
As an exercise, see Figure 2 and there’s a URL to where the image was obtained from. On that page, there are great-grandchildren…12 nodes (to-date). You can add these nodes with their names and titles (they are mostly babies/kids, so there may not be titles for everyone in that pool, but you can put “None” for title), and see if you can build that tree using the knowlege already shared here. They will be at level 3. It’ll be just few lines of code only to add to more nodes, all the methods and functions should not need any modification…but try it yourself.
Hope this was fun and informational.
By the way, if you want how to do true graphical representation with color-coding, shapes, lines, then check out my blog post on network graphs here.
▛Interested in creating programmable, cool electronic gadgets? Give my newest book on Arduino a try: Hello Arduino! 
▟
sdfdsfsdf
sdfsd
fsd
fsdf
df
sdf
dsfsd
fsd