Derivatives are used to find the rate of changes of a quantity with respect to another quantity. The derivative of a variable tells us the rate of change of a function’s output value as it varies from the initial value…how much is it changing?
For a straight line (e.g. linear regression), we can calculate the rate of change of a y variable (say, on y-axis) based on the x values (say, on x-axis) using linear regression or slope formula. Which basically says, at any given value for x we can predict vaule of y (aka y hat) based on the regression or slope formula: y=mx+b. But when we have a curve and not a linear regression, we cannot use slope formula, we have to use derivatives (for single variable) or partial derivatives (for multivariate situations with >=2 vars)…a Calculus concept.
The derivative of a function at some point tells us how the rate of change of one or more variables affect the change in another value (e.g. to predict, usually called y…y is the known values for training in Machine Learning (ML); and y hat is the predicted value of y solved by ML or neural network for example. The process of finding the derivatives in calculus is called differentiation.
Application of derivatives in real life:
- Calculate the profit and loss
- Check the temperature variation
- Speed or distance covered
- Range of magnitudes of earthquakes
- Change in price due to size of a house
- Income change due to age and so much more!
And that’s just the simple derivative applications with a single dependent variable. Then we can go into more complex non-linear regression involving multivariate scenarios such as how size, age, location affect the price of a house, and much more. That is when we whip out partial derivatives. For partial derivatives involving multiple vars, we have to specify the derivative is with respect to which single variable.
Of course, you can refer back to your school notes and compute the derivatives by hand (manually). However, once you do, you can optimize that process further by letting the computer do the work for any equation without wracking your brain each time. In this example, I show a few examples of how to calculate derivatives and partial derivatives using code (Python) very efficiently. You’ll need Python 3.x and preferrably Jupyter notebook for the decorated outputs like in Latex but you can use another IDE and the results will be the same albeit not as decorated. For installation of Python and setting up your favorite IDE such as Visual Studio, IDLE, Thonny, Sublime, Jupyter, etc. (there are many!) you’ll need to search for these names and follow the specific directions for your platform. That is not in the scope of this blog.
Let’s recap the concept of a simple derivative.
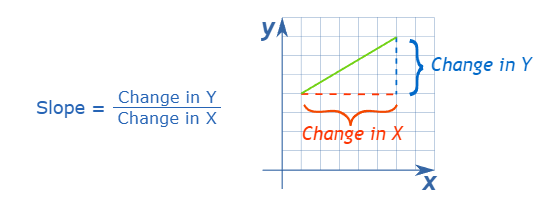
Then what’s a derivative of 9? At a given point, there’s no change in x or y! So the derivative is 0.
Then what’s the derivative of x^3 (x cubed)? It is 3x^2 (3 times x squared)…to refresh your memory, it’s one of the simplest rules to employ: we take the exponent, and put it as a coefficient before the variable x and then deduct 1 from the exponent and raise x to that power.
As the functions get more complex and multiple variables are introduced, it can get tedious to do it by hand, and that’s where we can use Python (or your favorite language) to do it for us.
So, let’s get started with coding.
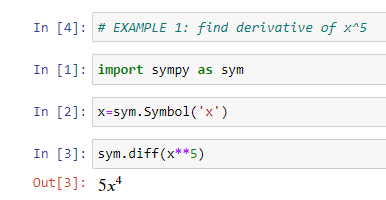
We import sympy library which makes doing differentials really easy with sympy.diff() function as shown above. In Jupyter notebook (not necessarily in other IDEs), the output actually shows superscripts for power nicely!
Let’s look at more examples…
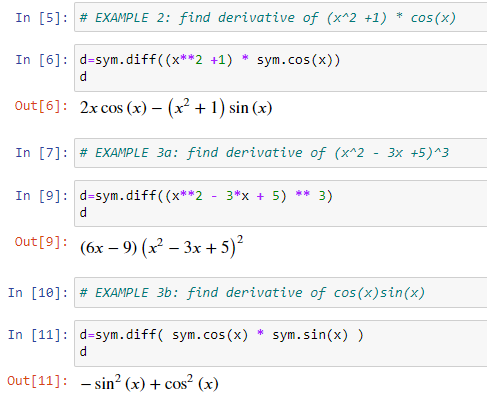
There were using a single variable (x). What if we have multiple variables? Then we use partial derivatives as mentioned above, and the way to do it in code is shown below.
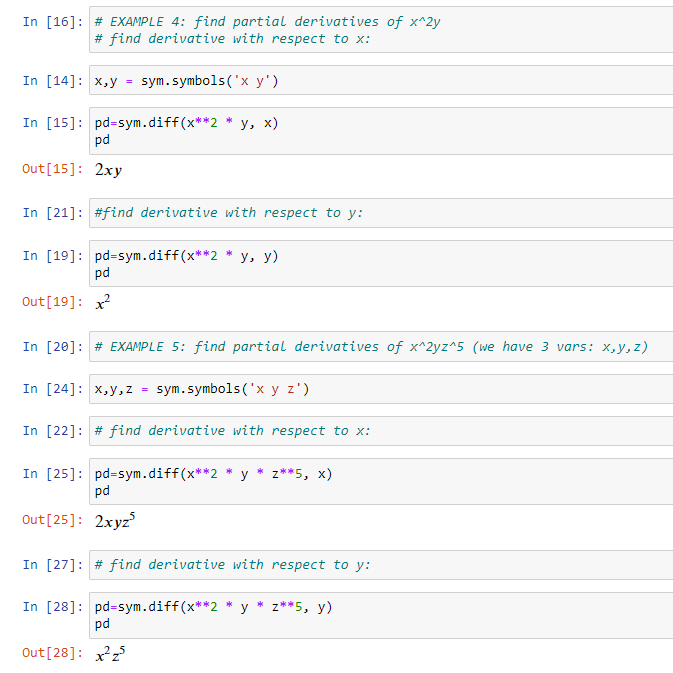
For each variable, we define them using Symbol() for single variable or symbols() for multiple variables. Using this method, we can tackle as many variables as we want. To keep things simple, I re-typed the function each time for each partial derivative above, but we could refactor our code by simply defining the function as a variable and only referring to the variable instead of re-typing the entire function for each partial derivative. Below is an example how we can do this (wrt=with respect to):
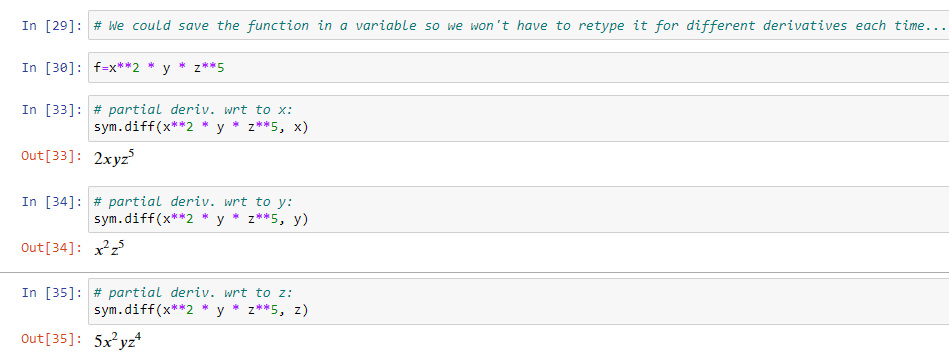
I hope this raised your curiosity a bit and was helpful.
▛Interested in creating programmable, cool electronic gadgets? Give my newest book on Arduino a try: Hello Arduino! 
▟