Today, I present a real-life problem that actually goes back many years in terms of the type of problem and method to tackle such. Here’s the scenario:
There was a robbery and the software has identified the perpetrator to be black. The case goes to jury and they must decide with the help of the prosecutor and defense attorney. But one of the attorney have consulted an analyst to help present the case based on the following facts gathered: The demographics of that town is: 70% white, 30% black. The software correctly recognizes a persons’ faces correctly 90% of the time.
You are the analyst who needs to present quantitative facts based on the known. What’s your finding?
The Process & Solution:
Probability that the identification is correct is 90% (probability of being incorrect therefore is 10%…we’ll also need this number in our calculation later). Probability of being white of any one person is 70% (therefore, probability of being black is 30%…we’ll need this number as well).
The next thing you need to do is create a matrix of all possible outcomes and probability of each outcome. So, create a matrix as below:

Then your task is to finally find the actual numbers to fill in the matrix and only then you are able to answer the following accurately:
a) What’s the probability a person was actually black and software said he was black?
b) What’s the probability a person was actually white and software said he was white?
Let’s get started with the matrix. The math parts are very simple, however, it requires understanding of the Bayesian Theory in order to lay out the data properly so we can get the accurate answers. I won’t get into the theory here (it can be easily searched online), nor into the basic statistical concepts needed to apply Baye’s rule correctly (if interested, you may want to look into probabilities and permutations), but I’ll share the process and my results here.
So, the intersection of identified white and actually white is= 63% (because, accuracy*probability of white). Similarly, the probability where identified as black and actually black = 27%. Notice, these 2 add up to the best accuracy possible for the software: 90%. This covers the probabilities of the software when it’s CORRECT!
How about it’s inaccuracy probabilities in the matrix? The likelihood of an actual white person being identified as black = 7% (because inaccuracy*probability of being black). Similarly, the likelihood of an actual black person being identified as white = 3%. Notice, these add up to the inaccuracy of the software: 10%
Now your matrix looks like this:
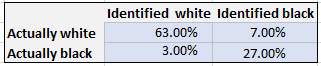
This is all you need but it might not make much sense for the attorney quite yet. So, you need to turn this into a more meaningful fact so that you can deliver the answers to a) and b) as I stated above. To do that, one more level of calculation…
Probability the robber was actually black and software said he was black: 79%. Put another way, software is 79% accurate if it said the robber was black. [how? 27% / (7% + 27%)]
And probability that the robber was actually white and software said he was white: 95%. Put another way, software is 95% accurate if it said the robber was white. [how? 63% / (63% + 3%)].

And that’s exactly where we just applied the Bayesian Theorem to come up with the answer.
Now, you’re not a lawyer, you’re an analyst, this is all you should and can provide and hope the lawyer presents the case without bias and the jury makes the right decision. I think Lt. Columbo would approve!
A spin: What if the software recognition software was replaced with a human witness’s account? And her identification accuracy was the same as the recognition software’s?
A FRIENDLY WARNING: Be sure to be accurate when calculating such measures, and always be 100% ethical when dealing with statistics/AI/analytics.