No, I’m not talking about stingy, spiteful kind…rather mathematical mean: arithmetic and statistical means to be exact. In fact, a handful of mean functions and applications. In most common situations, when we say ‘Mean’ even the statisticians mean the Average…or the arithmetic mean we all know since early childhood. We continue use it because while it’s so simple, it’s also very useful in most real-world applications. However, there are times it doesn’t quite cut it right! Here I show a tiny example of such.
Let’s say we have a dataset of different weights of cargo.
 Taking a simple arithmetic average of these values would yield 24,852. But is this really what we’re after? Does it really tell the whole story of what weights were used in this time-period or events? They’re same units but appear to have at least one or more outlier. The maximum value and the minimum values are highlighted in the dataset to demonstrate this. If we quickly analyze the data we find a large spread of the data as shown in the following stats:
Taking a simple arithmetic average of these values would yield 24,852. But is this really what we’re after? Does it really tell the whole story of what weights were used in this time-period or events? They’re same units but appear to have at least one or more outlier. The maximum value and the minimum values are highlighted in the dataset to demonstrate this. If we quickly analyze the data we find a large spread of the data as shown in the following stats:
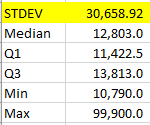 and therefore a very large variance of 939,969,281.
and therefore a very large variance of 939,969,281.
We can then chart it and quickly point out the outlier as shown as a dot below (X is the arithmetic mean) and show that there’s a large discrepancy between the outlier and the mean:
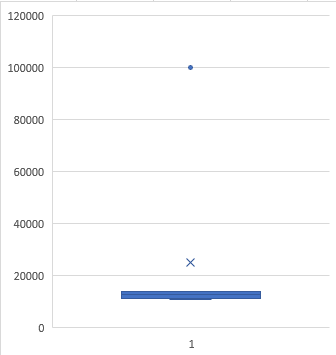
Fortunately, we have additional and ‘smarter’ ways to calculate mean or averages. A geomean or a harmonic mean are good for tackling this type of data. They use different ways to reduce the impact of outliers. For example, geomean will normalize the data and reduce the skewness in dataset where they can expect unpredictable data (that need to be accounted for) or data with large variance. Geometric mean can only be calculated for positive numbers. The general formula for the geometric mean of n numbers is the nth root of their product. The harmonic mean is the reciprocal of the arithmetic mean of the reciprocal values (1 over). Because of the way they determine their means, the Harmonic mean is always less than the Geometric mean, which is always less than the Arithmetic mean.
Then there’s another nifty mean method at our disposal, which allows us to selectively remove certain percentage of the data points from the dataset and calculate the mean! This is called TrimMean.
They can be calculated by hand or with any statistical software or even simpler, using Excel or Python. Let’s use the same dataset and calculate the different means in Excel usng AVERAGE(), GEOMEAN(), HARMEAN(), TRIMMEAN(). The output is below (let’s focus on the left Data column, I’ll get to the Ratio Data soon).
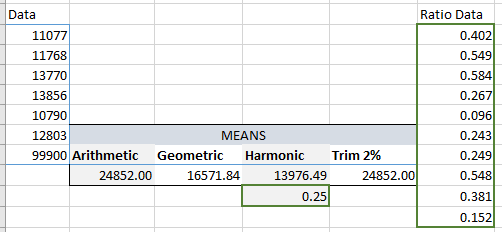
This is now clear that there was about 2% outlier in the dataset and trimming of which results in the mean being same as the arithmetic mean! However, that doesn’t necessarily mean we should remove the outliers! Outliers can be a pain or can be critical…it all depends on the research and purpose of the analysis. So, we find the Geo and Harmonic means as well accounting for skewness.
Let’s compare now the different means visually:
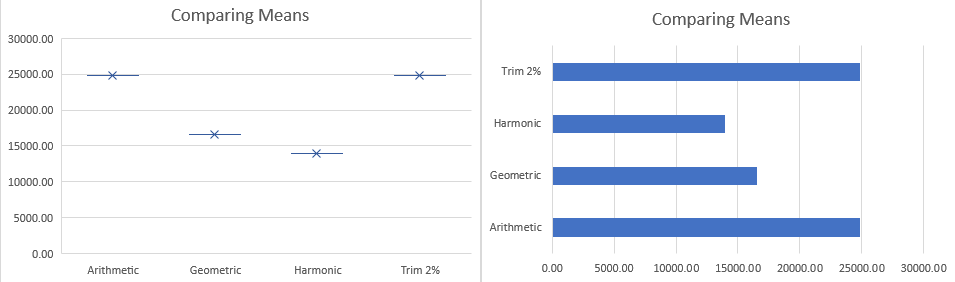
I would definitely be tending to stay within Geo and Harmonic ranges if the purpose for predictive analysis of weights.
Let me also quickly show you how you can calculate them in Python:
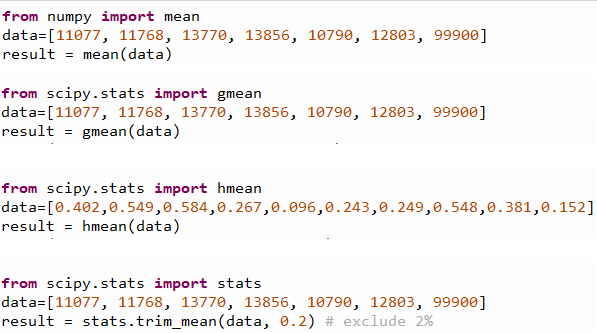
and the outputs are:

The outputs from Excel and Python are identical for all these calculations. Typically, we will use Harmonic mean if values are rates/ratios. That’s why I use the Ratio Data column above to compare Excel and Python outputs…again, they generated the accurate and same harmonic values.
Hope it was fun and interesting!
▛This post is not meant to be a formal tutorial, instead it is to offer key concepts, and approaches to problem-solving. Basic->Intermediate technical/coding knowledge is assumed. If you like more info or source file to learn/use, or need more basic assistance, you may contact me at tanman1129 at hotmail dot com. To support this voluntary effort, you can donate via Paypal from the button in my Home page, or become a Patron via my Patreon site. A supporter/patron gets direct answers on any of my blogs including code/data/source files whenever possible. At the very least, it’ll encourage me to share more posts/tips/knowledge in the future.▟