One of today’s most recognized physical laws is Murphy’s Law…one of the seeming fundamental laws of mankind: “If anything can go wrong, it will.”
In this post, I discuss its brief history, and entertain the attempt of mathematically formulating his maxim in order to apply to some real-world sitations.
The history:
The adage or truism, if you would, gained its popular name at Edwards Air Force Base (in California) in 1949 when Air Force Dr. John Paul Stapp pulled 40Gs during deceleration testing and lived to tell about it in a press conference. He attributed the project’s good safety record was based on a firm belief in Murphy’s Law and hence the necessity to circumvent it. Capt. Edward A. Murphy, an engineer working on the project (to see how much sudden deceleration a person can tolerate) had coined the “law” and it had become a metaphor for thoroughness in the project team.

Some corollaries of Murphy’s Law:
- A library book will always be checked out when you want to get it.
- All the good ones are taken.
- If it’s too good to be true, it probably is.
- If the person isn’t taken, there’s a reason.
- The nicer someone is, the farther away (s)he is from you.
- Brains x Beauty x Availability = Constan
- If there is a possibility of several things going wrong, the one that will cause the most damage will be the one to go wrong.
- The hidden flaw never stays hidden for long.
- Murphy’s Law of Thermodynamics: Things get worse under pressure.
- The Murphy Philosophy: Smile…tomorrow will likely be worse.
- Matter will be damaged in direct proportion to its value.
- Everything takes longer than you think.
- Every solution breeds new problems.
- The probability of an event occurring is inversely proportional to the desirability of that event.
- Murphy’s Tech: New systems generate new problems.
- Murphy’s Commerce Law: To err is human, to forgive is not company policy.
- Education: You never catch on until after the test.
- Murphy’s Mothers Laws: Mother’s way is best. If you don’t believe it, ask her.
- Office Laws: When you don’t have much work… all your colleagues will be busy.
- Horse Laws: Horses you hate cannot be sold and will outlive you.
After some research, I discovered that some experts have formulized the axiom to something as:
Pm = -Km (e ^ -((I*C*U) +F) /Fm) – 1)
Pm is Murphy’s Probability. Km is Murphy’s constant (equal to 1) and Fm is Murphy’s factor, a very small number …we can approximate it by FM ≈ 0.01. F is the frequency (not the same as Fm) and will vary by scenario as shown in examples below.
I is the importance of the result or outcome of the event, C is the complexity of the system, U is the urgency and F is the frequency. From these I, C, U, F parameters, virtually any event can be described. Plugging those numbers into the equation with the appropriate constants will then give the probability of at least one thing going wrong. The e is Euler’s number, is a mathematical constant approximately equal to 2.72.
Let’s calculate the probabilities and usefulness of the formula…
EXAMPLE 1: Lets calculate the probability of the clutch on a 1989 Toyota Tercel ceasing to function 50 miles from home at night in the middle of a rainstorm.
SOLUTION: The importance of the clutch working in this situation is obviously high, but no one is dying, so let’s say I=8. The clutch is fairly simple compared to other systems in the car, so C=5. It would be nice if the clutch worked soon, so set the urgency U=8. Finally, the clutch only needs to work for one drive home, so the frequency is one event meaning F=1. Now, putting these parameters in Murphy’s Equation shows that PM=1. Meaning, it’ll definitely happen!

EXAMPLE 2: Moving to a more complicated example, let’s examine the case where the clutch has failed in the above example, but calculate the probability that the flashlight needed to inspect the clutch doesn’t work, the car emergency lights don’t work and that the trunk where tools are kept won’t open.
SOLUTION: In this case, Importance is about the same, an 8 or so (its hard to justify higher than this without a life or death situation). Here, C=4, as the flashlight, emergency lights and trunk are all fairly simple systems by themselves. Because it is raining and the driver is now stranded, the urgency can be bumped up to a 9, and this time F=3 (three events need to occur: flashlight, emergency lights, trunk).
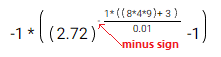
or in natural language: -1 * (Power[2.72,- 1* ((8*4*9)+ 3 ) /0.01] -1)
Again, we see the likelihood of it occuring is very high. When and who it’ll happen to is another story 😊
Remember to smile today…tomorrow will likely be worse ¯_(ツ)_/¯